Transformada de Laplace

La Transformada de Laplace de una función matemática f(t) definida para todos los números reales t ≥ 0 es la función F(s), definida por:



Cuando se habla de la transformada de Laplace, generalmente se refiere a la versión unilateral. También existe la transformada de Laplace bilateral, que se define como sigue:




La transformada de Laplace F(s) tipicamente existe para todos los números reales s > a, donde a es una constante que depende del comportamiento de crecimiento de f(t).

Aplicacion en la ingenieria electronica

Gracias a la transformada de Laplace se pueden resolver muchos circuitos, los cuales son muy difíciles de resolver en el dominio del tiempo. Un ejemplo de esto son los circuitos con múltiples inductancias y condensadores, ya que por cada uno de estos componentes que se agregue, la ecuación resultante es una ecuación diferencial de mayor orden. Al transformar este tipo de circuitos al dominio de Laplace las ecuaciones se simplifican considerablemente y es posible resolverlas en ese dominio, para después llevarlas al dominio del tiempo resueltas.

Definiciòn De La Serie De Fourier

A continuacion se mostrara la definiciòn de la serie de fourier aplicada a las señales senoidales

Las Series De Fourier En Señales Alternas

Una serie de Fourier es una serie infinita que converge puntualmente a una función continua y periódica. Las series de Fourier constituyen la herramienta matemática básica del análisis de Fourier empleado para analizar funciones periódicas a través de la descomposición de dicha función en una suma infinitesimal de funciones senoidales mucho más simples (como combinación de senos y cosenos con frecuencias enteras). El nombre se debe al matemático francés Jean-Baptiste Joseph Fourier que desarrolló la teoría cuando estudiaba la ecuación del calor. Fue el primero que estudió tales series sistemáticamente, y publicando sus resultados iniciales en 1807 y 1811. Esta área de investigación se llama algunas veces Análisis armónico.

Las Señales Electricas Senosoidales

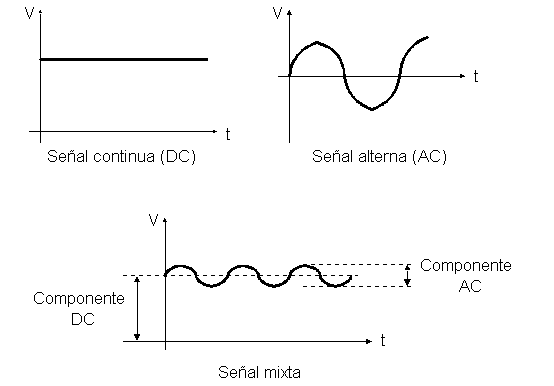
Una señal senosuidal, trata de una señal analógica, puesto que existen infinitos valores entre dos puntos cualesquiera sea el dominio. Así pues, podemos ver en la imagen que la onda describe una curva continua. De hecho, esta onda es la gráfica de la función matemática seno, que posee los siguientes atributos característicos:

*La función seno está perfectamente definida mediante su expresión analítica y gráfica. Mediante la teoría de los números complejos se analizan con suma facilidad los circuitos de alterna.


*Las ondas periódicas no senoidales se pueden descomponer en suma de una serie de ondas senoidales de diferentes frecuencias que reciben el nombre de armónicos. Esto es una aplicación directa de las series de Fourier.

Aplicacion De La Integral En La Electronica

En el area de la ingenieria electronica la aplicacion de las integrales es bastante amplia,desde utilizarla en circuitos pequeños hasta la aplicabilidad dentro del area industrial por ejemplo, la cantidad de consumo en WATT(vatios)